Raumakustik

Dieses Kapitel ist noch nicht vollständig.
Ergänzungen dazu folgen bald.

Die Raumakustik eines Raums wird primär daran gemessen wie dieser Raum auf bestimmte Frequenzen reagiert und wie schnell diese Frequenzen nach Anregung wieder abklingen, also der frequenzbasierte Nachhall. Aber nicht nur das reine Analysieren und Beeinflussen dieser Faktoren gehört dazu. Auch sind sogenannte early reflections von großer Bedeutung, also frühe Reflektionen, insbesondere von den seitlichen Wänden sowie das allgemeine Abstrahlverhalten und die Schallausbreitung.

In diesem Post soll es daher allgemein um Raummoden, die Reflektionsfreie Zone sowie Soffit-Mounting gehen.

1 | Raummoden

Raummoden sind ein Phänomen in rechteckigen Grundrissen bzw. in geschlossenen quaderförmigen Räumen. Eine Raummode ist dabei die stehende Welle zwischen zwei oder mehreren paarweise parallelen Wänden. Die Frequenz der stehenden Welle wird abhängig von der Abhörposition im Raum verstärkt, verringert oder ganz ausgelöscht wahrgenommen. Kennen tun wir dieses Phänomen z.B. beim Musikhören oder Filmgucken wenn manche Bassfrequenzen stark überbetont werden und der ganze Raum dröhnt, andere aber wiederum ganz verschluckt werden.

Dieser Effekt tritt bei allen Vielfachen der Frequenz der stehenden Welle, jedoch mit absteigender Intensität bei steigender Frequenz. Die Vielfachen dieser Frequenz werden im Allgemeinen Oberwellen und im Speziellen Raummode erster Ordnung, zweiter Ordnung, usw. genannt. Die Grundfrequenzen sind hierbei am wichtigsten, da sie am stärksten ausgeprägt sind. Relevante Raummoden befinden sich generell unterhalb von 200 Hz (manche sagen 300 Hz). In nachfolgendem Bild sieht man eine Raummode und ihre Oberwellen (Raummode 1. Ordnung – 6. Ordnung):

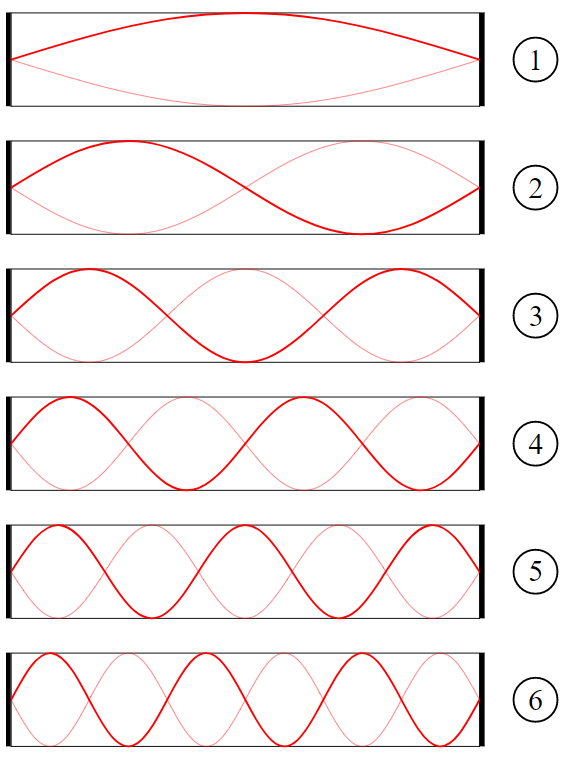
Die Frequenz einer Raummode für ein Wandpaar mit dem bekannten Wandabstand a errechnet sich wie folgt:

$f = \frac{c}{2 \cdot a}$

Dabei ist c die Schallgeschwindigkeit. Der Wert für die Schallgeschwindigkeit ist von diversen Faktoren abhängig, z.B. von der Temperatur. Ich nehme idR. 343. Manche rechnen, aber auch mit 340 oder 344.

Genauer gesagt ist dies die Frequenz einer axialen Mode. Es gibt nämlich gleich 3 Arten von Moden: Axial (oder longitudinal), tangential und oblique (oder diagonal oder schräg). Axiale Moden entstehen zwischen zwei parallelen Wänden. Tangentiale Moden entstehen zwischen vier Wänden, welche jeweils paarweise parallel zu sind, also z.B. zwischen linker Wand, rechter Wand, Boden und Decke. Oblique Moden entstehen zwischen sechs Wänden, also in einem quaderförmigen Raum zwischen allen vorhandenen Oberflächen.

Alle 3 Raummodenarten lassen sich über folgende Formel berechnen:

$f = \frac{c}{2} \cdot \sqrt{(\frac{n_x}{L_x})^2+(\frac{n_y}{L_y})^2+(\frac{n_z}{L_z})^2}|n \in \mathbb{N} = 1, 2, 3, ...$

Dabei sind Lx, Ly, Lz die Raumabmessungen, also Länge, Breite, Höhe in Metern. Die jeweilige Ordnung der Mode bezeichnet n.

1.2 Beispielberechnung

Aufnahmeraum und Regie werden bei uns nicht rein quaderförmig. Als Beispiel nehmen wir daher unseren geplanten Eingangsbereich/Lobby, da dieser vollständig quaderförmig sein wird. Der Raum ist 373,82m lang und 238,59m breit. Die Deckenhöhe beträgt 2,50m.

1.2.1 Axiale Moden

1.2.1.1 Axiale Moden erster Ordnung

$\\f^{\text{axial}}_{\text{1. Ordnung}} = \frac{343}{2} \cdot \sqrt{(\frac{1}{373,82})^2+(\frac{0}{238,59})^2+(\frac{0}{2,50})^2} \approx 45,88 \text{ Hz} \\f^{\text{axial}}_{\text{1. Ordnung}} = \frac{343}{2} \cdot \sqrt{(\frac{0}{373,82})^2+(\frac{1}{238,59})^2+(\frac{0}{2,50})^2} \approx 71,88 \text{ Hz} \\f^{\text{axial}}_{\text{1. Ordnung}} = \frac{343}{2} \cdot \sqrt{(\frac{0}{373,82})^2+(\frac{0}{238,59})^2+(\frac{1}{2,50})^2} = 68,60 \text{ Hz}$

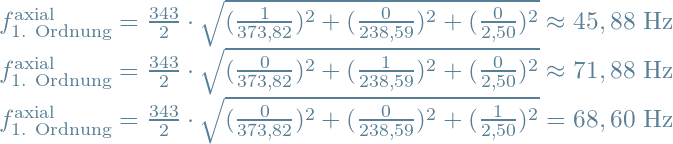
1.2.1.2 Axiale Moden zweiter Ordnung

$f^{\text{axial}}_{\text{2. Ordnung}} = \frac{343}{2} \cdot \sqrt{(\frac{2}{4})^2+(\frac{0}{3})^2+(\frac{0}{2,50})^2} \approx 91,76 \text{ Hz} \\f^{\text{axial}}_{\text{2. Ordnung}} = \frac{343}{2} \cdot \sqrt{(\frac{0}{4})^2+(\frac{2}{3})^2+(\frac{0}{2,50})^2} \approx 143,76 \text{ Hz} \\f^{\text{axial}}_{\text{2. Ordnung}} = \frac{343}{2} \cdot \sqrt{(\frac{0}{4})^2+(\frac{0}{3})^2+(\frac{2}{2,50})^2} = 137,20 \text{ Hz}$

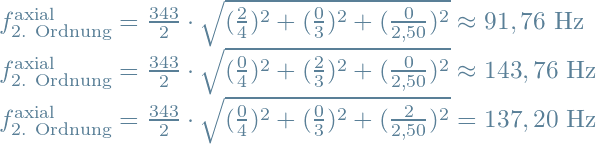
1.2.1.3 Axiale Moden i-ter Ordnung

Einfacher ist ab der zweiten Ordnung weitere Ordnungen als einfache Vielfache davon zu berechnen. Also:

$f^{\text{axial}}_{\text{i. Ordnung}} = i \cdot f^{\text{axial}}_{\text{1. Ordnung}}|i \in \mathbb{N}$

1.2.2 Tangentiale Moden

1.2.2.1 Tangentiale Moden erster Ordnung

Hier müssen jeweils zwei n ungleich 0 gesetzt sein.

$f^{\text{tangential}}_{\text{1. Ordnung}} = \frac{343}{2} \cdot \sqrt{(\frac{1}{373,82})^2+(\frac{1}{238,59})^2+(\frac{0}{2,50})^2} \approx 85,27 \text{ Hz}$

(Länge und Breite)

$f^{\text{tangential}}_{\text{1. Ordnung}} = \frac{343}{2} \cdot \sqrt{(\frac{0}{373,82})^2+(\frac{1}{238,59})^2+(\frac{1}{2,50})^2} \approx 99,36 \text{ Hz}$

(Breite und Höhe)

$f^{\text{tangential}}_{\text{1. Ordnung}} = \frac{343}{2} \cdot \sqrt{(\frac{1}{373,82})^2+(\frac{0}{238,59})^2+(\frac{1}{2,50})^2} = 82,53 \text{ Hz}$

(Länge und Höhe)

1.2.2.2 Tangentiale Moden i-ter Ordnung

Berechnungen tangentialer Moden i-ter Ordnungen erfolgt analog zu axialen Moden i-ter Ordnung.

1.2.3 Oblique Moden

Hier müssen alle n gesetzt sein.

1.2.3.1 Oblique Mode erster Ordnung

$f^{\text{oblique}}_{\text{1. Ordnung}} = \frac{343}{2} \cdot \sqrt{(\frac{1}{373,82})^2+(\frac{1}{238,59})^2+(\frac{1}{2,50})^2} \approx 85,27 \text{ Hz}$

(Länge + Breite + Höhe)

1.2.3.2 Oblique Moden i-ter Ordnung

Berechnungen obliquer Moden i-ter Ordnungen erfolgt analog zu axialen und tangentialer Moden i-ter Ordnung.

1.3 Praxis und Anwendbarkeit von Raummoden

Allgemein und vor allem in kleinen Räumen sind tangentiale und insbesondere oblique Moden oft vernachlässigbar. Auch besitzen Räume, welche nicht würfel- oder quaderförmig sind diese Raummoden nicht in dieser Form.

Raummoden dieser Art kann man durch schräge, nicht-parallele Wände zwar vermeiden, man erzeugt jedoch andere Resonanzfrequenzen bzw. stehende Wellen durch schräge Wände. Diese sind dann im Gegensatz zu den 3 Raummodenarten jedoch schwer vorherzusagen. Oft erzeugt man damit eine Vielzahl möglicherweise problematischer Moden, welche man später aufwändig messen und einzeln behandeln muss, um die Raumakustik homogen zu gestalten. Oft ist es tatsächlich eine gute Entscheidung einen Raum ganz bewusst mit Raummoden zu gestalten, sodass man sie später gezielt und punktgenau behandeln kann als einen ganzen Frequenzbereich behandeln zu müssen.

In unserem Fall (Aufnahmeraum und Regie) gibt es keine eindeutigen Raummoden durch parallele Wände, da wir keine quaderförmigen Räume haben. Dennoch gibt es einige parallele Wandpaare, welche diverse stehende Wellen hervorrufen können. Diese sind jedoch weit schwächer ausgeprägt.

Das nachfolgende Bild zeigt die entsprechenden parallelen Flächenpaare mit ihren entsprechenden Abständen und korrespondierenden Grundfrequenzen. Die farbliche Hinterlegung zeigt die zu erwartende Ausprägungsstärke anhand ihres Flächenanteils im Raum.

Die Frequenzen wurden dabei anhand der oben bereits erwähnten Formel erreichnet:

$f = \frac{c}{2 \cdot a}$

Bei einer Raummodenanalyse (die wie gesagt nur bei quaderförmigen Räumen sinnvoll ist) würde man jetzt diese Frequenzen sowie deren Frequenzen 1. Ordnung, 2. Ordnung, usw. bis 200 Hz (respektive 300 Hz) grafisch auflisten und schauen an welchen Stellen besonders viele Frequenzen beieinander liegen (--> mehrfache Verstärkung). Diese Frequenzen würde man später behandeln wollen. Ein Raummodenrechner dafür findet man z.B. -hier-.

Man sieht dass vermutlich besonders stehende Wellen mit ca. 47 Hz (und entsprechende Oberwellen: 95Hz, 142Hz und 190Hz) zwischen Böden und Decken recht ausgeprägt sein werden, weil sie flächenanteilig mit Abstand die größten parallelen Oberflächen sind. Maßnahmen hierfür könnten z.B. Slot Resonatoren oder Plattenschwinger für eben diese Frequenz sein. Durch das inside-out System der Wände bieten sich besonders erstere an, da diese ohne Raumverlust in die Wandtiefe integrierbar sind. Möglichkeiten bestimmte Frequenzen gezielt zu dämpfen möchte ich später in einem Kapitel zu Akustikelementen genauer beleuchten.

2 | Reflektionsfreie Zone

Die Reflektionsfreie Zone (kurz: RFZ) beschreibt einen Bereich, in dem ein Hörer nur den direkten Schall aus den Lautsprechern hören soll (schwarze Pfeile) und Reflektionen der Wände (insbesondere die sogenanten frühen Reflektionen, rote Pfeile) möglichst in den hinteren Teil des Raums geleitet werden sollen (blaue Pfeile), wo sie dann entweder kontrolliert reflektiert, absorbiert oder gestreut werden. Eine geeignete Reflektionsumleitung kann durch gewinkelte Wände umgesetzt werden. Um die RFZ zu bestimmen muss man ein Ray Tracing („Strahlenverfolgung“) ausführen und anhand interessanter Abstrahlungen ermitteln wohin die Schallausbreitung stattfindet.

Die RFZ muss eigentlich in 3D bestimmt werden, allerdings habe ich eine 2D-Version auf Hörebene (im Sitzen) erstellt, um die 2D-Maße des Regieraums zu bestimmen bzw. zu verbessern. Sie ist die Begründung für das aktuelle Layout des Regieraums. Grundannahme hierbei ist, dass die Rückwand absorbierend ist und Schall dort nicht oder nur stark reduziert weiterreflektiert wird. Die Abhörposition befindet sich bei 39% des Raumtiefe (37% ist ideal). Wegen der Übersichtlichkeit folgt vorerst eine Version nur für den linken Lautsprecher:

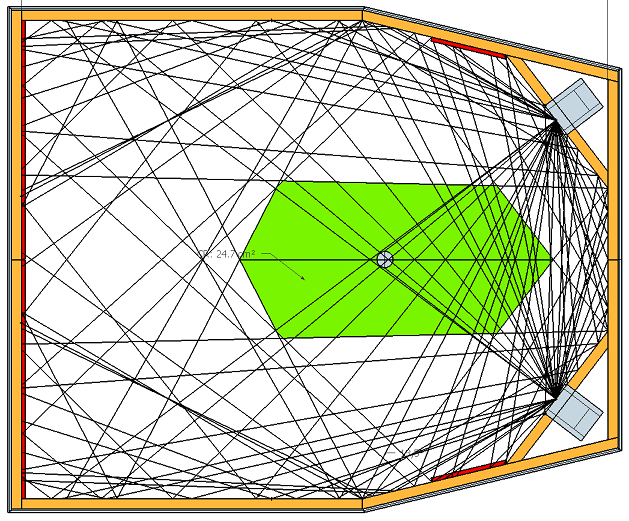
Jetzt eine Version für beide Lautsprecher. Die grüne Fläche zeigt die resultierende reflektionsfreie Zone an. Man sieht, dass die Abhörposition recht nahe dem Ende dieser Fläche liegt.

Hier nun eine Version, in der Teile der seitlichen Wände absorbierend gestaltet sind (Im Bild rot). Die reflektionsfreie Zone vergrößert sich deutlich nach hinten hin.

Eine dreidimensionale Analyse und detaillierte Informationen folgen bald.

Akustik, Planung, Theorie